 最短路径:Dijkstra算法
最短路径:Dijkstra算法
# 概述
迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。迪杰斯特拉算法采用的是贪心策略,**将Graph中的节点集分为最短路径计算完成的节点集S和未计算完成的节点集T,每次将从T中挑选V0->Vt最小的节点Vt加入S,并更新V0经由Vt到T中剩余节点的更短距离,直到T中的节点全部加入S中,它贪心就贪心在每次都选择一个距离源点最近的节点加入最短路径节点集合。**迪杰斯特拉算法只支持非负权图,它计算的是单源最短路径,即单个源点到剩余节点的最短路径,时间复杂度为O(n²)。
# 算法描述
在有向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短值。
# 算法流程
本节将对算法流程进行模拟,设置Graph为包含7个顶点和9条边的有向无环图,源点为0,计算从源点0到剩余节点的最短路径,Graph如下:

每个节点将维护shortest和visited两个数据结构,shortest存储v0到该节点的最短路径,visited存储v0到该节点的最短路径是否求出。S为已求出最短路径的节点,T为未求出最短路径的节点。源节点只允许将S中的节点作为中间节点来计算到达其它节点的最短路径,不允许将T中的节点作为中间节点来计算到达其它节点的最短路径。随着S中节点的增加,源节点可达的节点才会增加。初始状态下,源节点只可达节点1和节点3。
# 算法步骤如下:
1、将源节点(即节点0)加入S中,对shortest和visited数组进行更新。
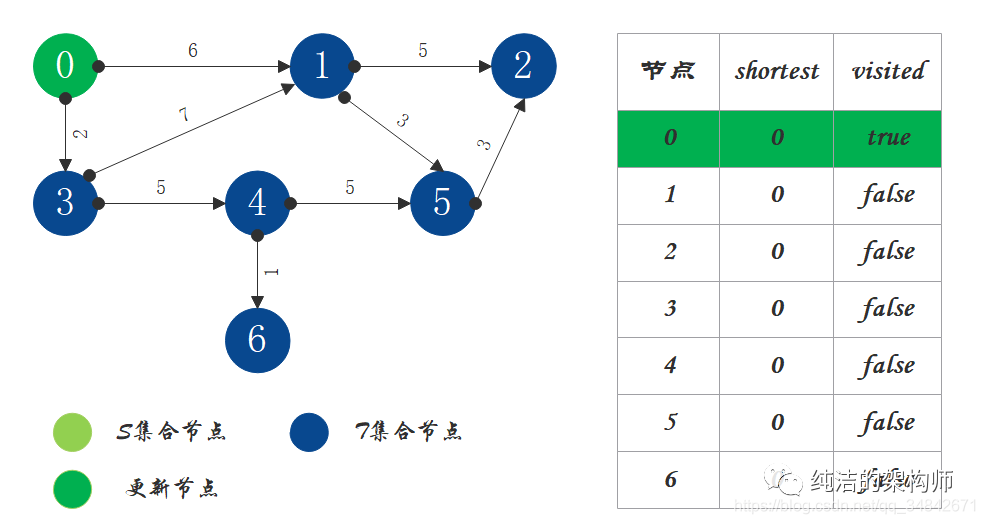
2、S中现有节点0,源节点可达T中的节点1和节点3,节点0->节点1距离为6,节点0->节点3距离为2,按距离从小到大排序,因此选择将节点3加入S中。更新源点将节点3作为中间节点到达其它节点的距离。
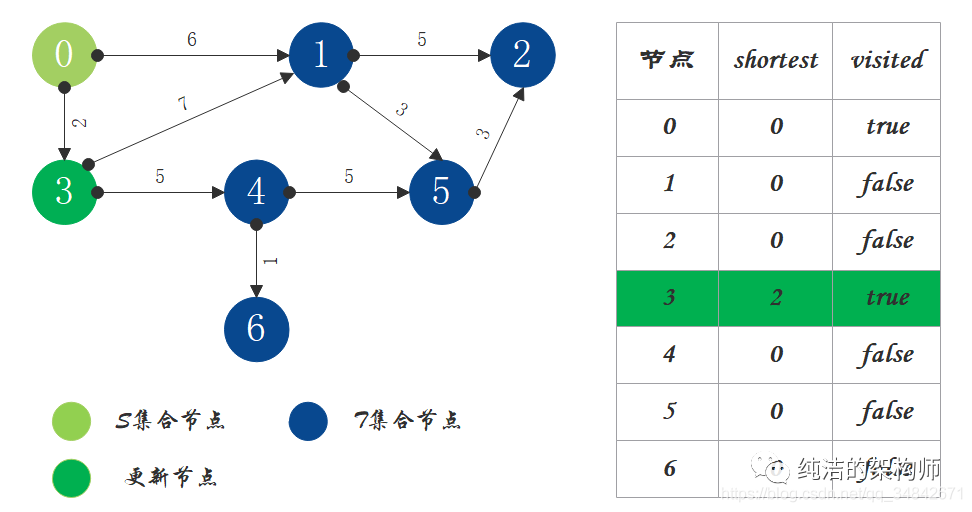
3、S中现有节点0和节点3,源节点可达T中的节点1和4,节点0->节点1距离为6,节点0->节点4距离为7,按距离从小到大排序,因此选择将节点1加入S中。更新源点将节点1作为中间节点到达其它节点的距离。
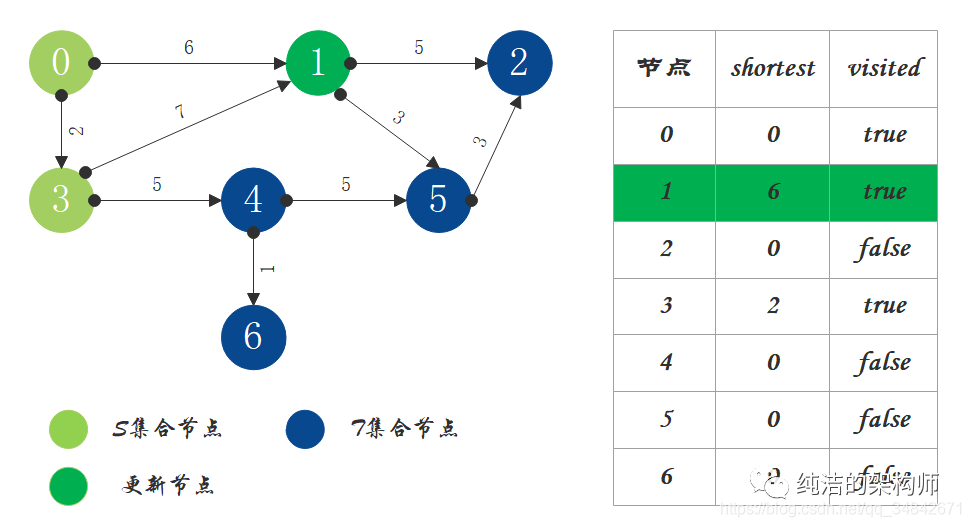
4、S中现有节点0、1、3,源节点可达T中的节点2、4、5,0->2距离为11,0->4距离为7,0->5距离为9,按距离从小到大排序,因此选择将节点4加入S中。更新源点将节点4作为中间节点到达其它节点的距离。
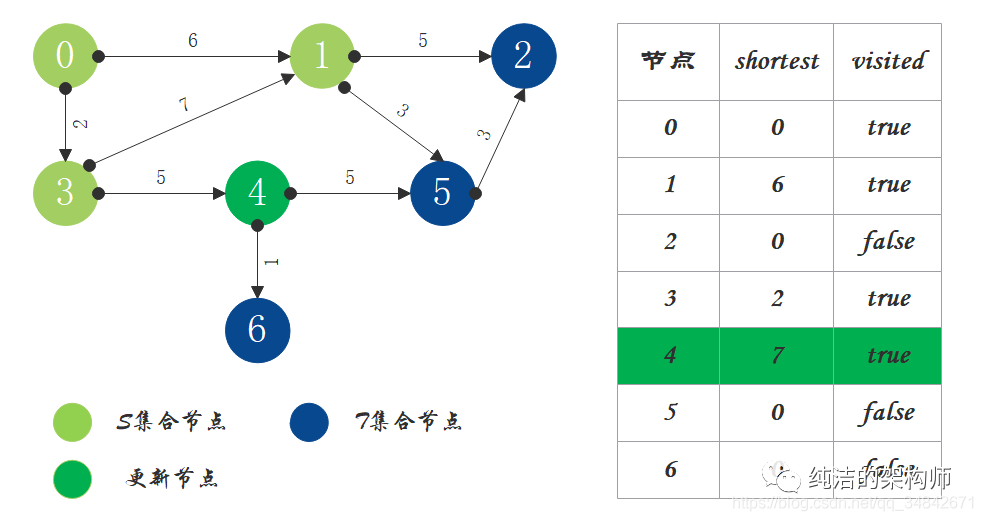
5、S中现有节点0、1、3、4,源节点可达T中的节点2、5、6,0->2距离为11,0->5距离为9,0->6距离为8,按距离从小到大排序,因此选择将节点6加入S中。更新源点将节点6作为中间节点到达其它节点的距离。
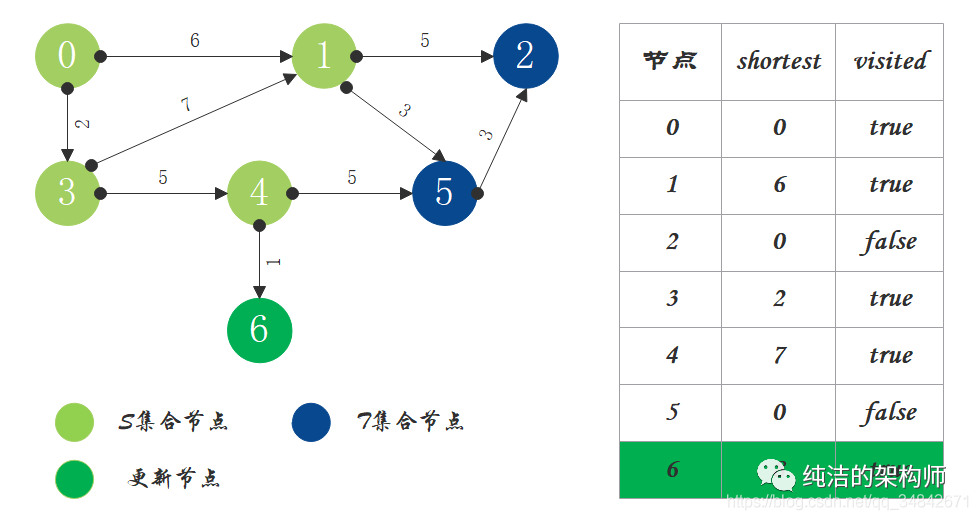
6、S中现有节点0、1、3、4、6,源节点可达T中的节点2、5,0->2距离为11,0->5距离为9,按距离从小到大排序,因此选择将节点5加入S中。更新源点将节点5作为中间节点到达其它节点的距离。
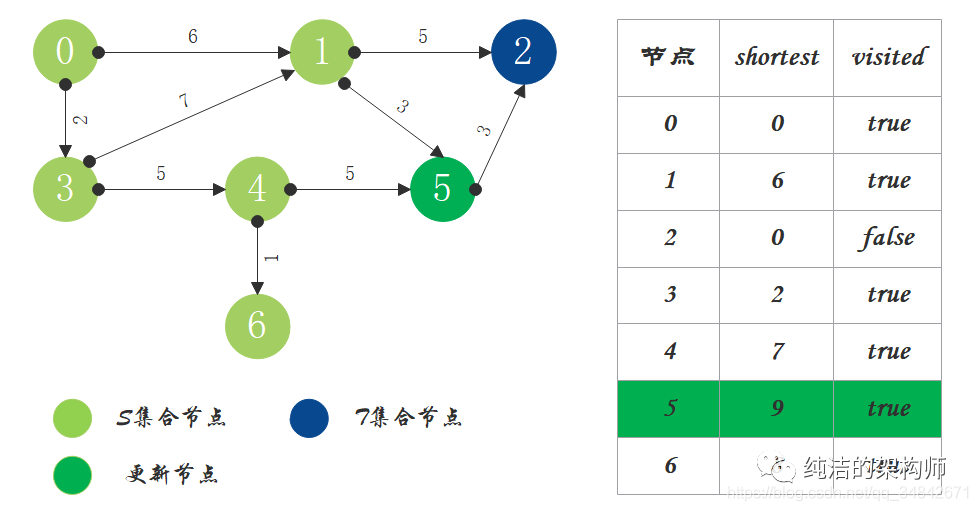
7、T中只剩下节点2,0->2距离为11,将节点2加入S中。
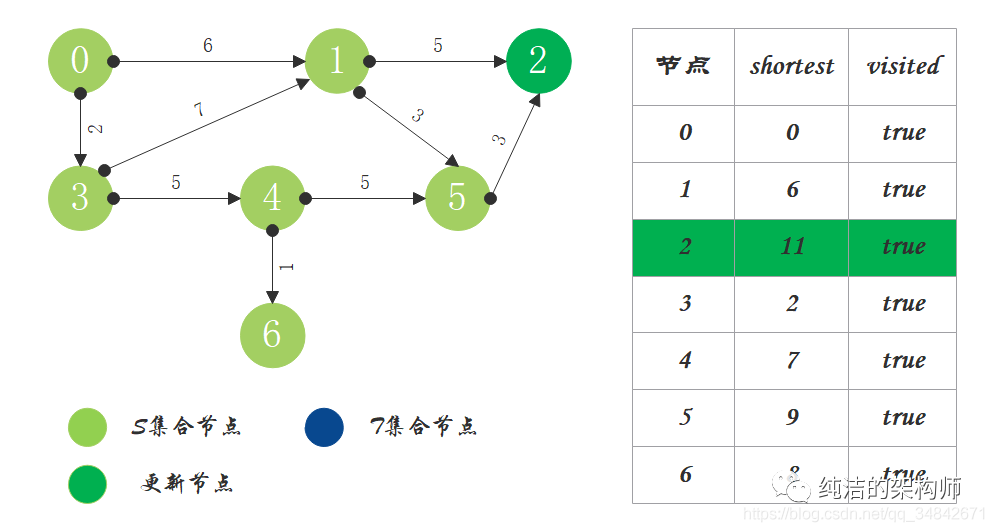
8、算法结束,源点到其它节点的最短路径都已依次求出。
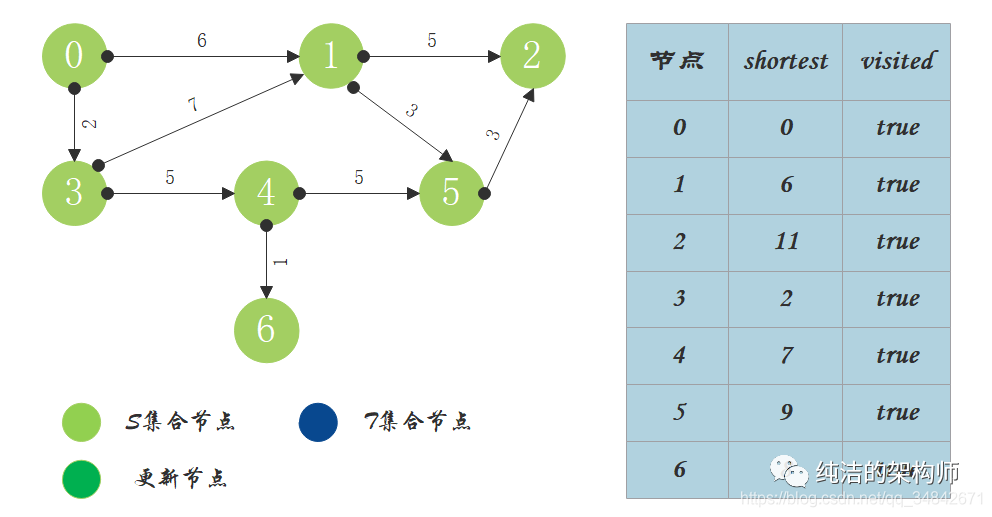
(下面一张图片出自该文章最上面那视频链接里面的内容,这里主要是看下面的图和表格,其他文字不全可能看不懂)
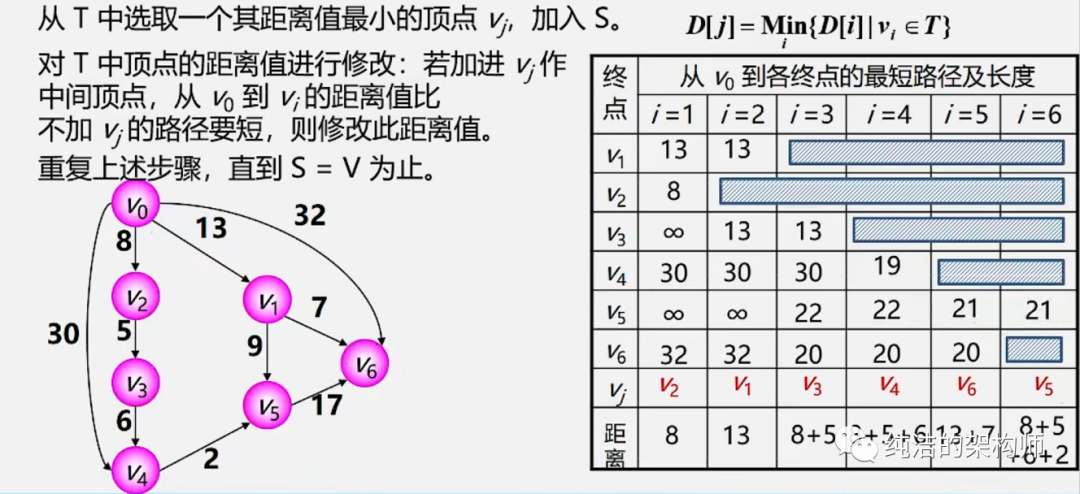
# 算法实现
public class DijstraAlgorithm {
//不能设置为Integer.MAX_VALUE,否则两个Integer.MAX_VALUE相加会溢出导致出现负权
public static int MaxValue = 100000;
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.println("请输入顶点数和边数:");
//顶点数
int vertex = input.nextInt();
//边数
int edge = input.nextInt();
int[][] matrix = new int[vertex][vertex];
//初始化邻接矩阵
for (int i = 0; i < vertex; i++) {
for (int j = 0; j < vertex; j++) {
matrix[i][j] = MaxValue;
}
}
for (int i = 0; i < edge; i++) {
System.out.println("请输入第" + (i + 1) + "条边与其权值:");
int source = input.nextInt();
int target = input.nextInt();
int weight = input.nextInt();
matrix[source][target] = weight;
}
//单源最短路径,源点
int source = input.nextInt();
//调用dijstra算法计算最短路径
dijstra(matrix, source);
}
public static void dijstra(int[][] matrix, int source) {
//最短路径长度
int[] shortest = new int[matrix.length];
//判断该点的最短路径是否求出
int[] visited = new int[matrix.length];
//存储输出路径
String[] path = new String[matrix.length];
//初始化输出路径
for (int i = 0; i < matrix.length; i++) {
path[i] = new String(source + "->" + i);
}
//初始化源节点
shortest[source] = 0;
visited[source] = 1;
for (int i = 1; i < matrix.length; i++) { //即图中表格横坐标
int min = Integer.MAX_VALUE;
int index = -1;
for (int j = 0; j < matrix.length; j++) { //表格纵坐标{
//已经求出最短路径的节点不需要再加入计算并判断加入节点后是否存在更短路径
if (visited[j] == 0 && matrix[source][j] < min) {
min = matrix[source][j];
index = j;
}
}
//更新最短路径
shortest[index] = min;
visited[index] = 1;
//更新从index跳到其它节点的较短路径(这步骤主要是为了循环下一个i准备的数据))
for (int m = 0; m < matrix.length; m++) {
if (visited[m] == 0 && matrix[source][index] + matrix[index][m] < matrix[source][m]) {
matrix[source][m] = matrix[source][index] + matrix[index][m];
path[m] = path[index] + "->" + m;
}
}
}
//打印最短路径
for (int i = 0; i < matrix.length; i++) {
if (i != source) {
if (shortest[i] == MaxValue) {
System.out.println(source + "到" + i + "不可达");
} else {
System.out.println(source + "到" + i + "的最短路径为:" + path[i] + ",最短距离是:" + shortest[i]);
}
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
样例输入:
请输入顶点数和边数:
7 10
请输入第1条边与其权值:
0 1 6
请输入第2条边与其权值:
1 2 5
请输入第3条边与其权值:
0 3 2
请输入第4条边与其权值:
3 1 7
请输入第5条边与其权值:
3 4 5
请输入第6条边与其权值:
1 2 5
请输入第7条边与其权值:
1 5 3
请输入第8条边与其权值:
4 5 5
请输入第9条边与其权值:
5 4 2
请输入第10条边与其权值:
4 6 1
0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
输出
0到1的最短路径为:0->1,最短距离是:6
0到2的最短路径为:0->1->2,最短距离是:11
0到3的最短路径为:0->3,最短距离是:2
0到4的最短路径为:0->3->4,最短距离是:7
0到5的最短路径为:0->1->5,最短距离是:9
0到6的最短路径为:0->3->4->6,最短距离是:8
2
3
4
5
6
Q&A
问:为什么迪杰斯特拉算法只支持非负权的图?
答:迪杰斯特拉采用的贪心策略,S集合中是已经计算出最短路径的节点,T集合中是未计算出最短路径的节点。假设存在负权,源点为A,已经计算出A->B的最短路径为m,若下一次将C添加进已计算出最短路径的节点集合,而A->C=m,C->B=-1,则会出现A->B的更短路径A->C->B,但迪杰斯特拉不会对已经计算出最短路径的节点重新计算,因此无法更新最短路径,即负权的出现导致无法保证S中节点计算的是最短路径,已经固定dis的点可能会被其它dis大于它的点更新。
问:为什么在代码实现中不能将节点之间不可达用Integer.MAX_VALUE代表?
答:因为两个Integer.MAX_VALUE相加会溢出导致出现负权,所以最好设置为一个比较大且不容易相加溢出的数。
问:迪杰斯特拉算法适用于什么场景?
答:在有些算法书上说,迪杰斯特拉适用于DAG(有向无环图)。但是个人觉得,它所谓的“适用于”,或许只是说可以在DAG上使用,并不代表无向图不能使用,也不能代表有环图不能使用。从迪杰斯特拉的算法原理上来说,无向图是没有问题的,只需要给matrix[source][target]和matrix[target][source]赋上相同的权值,因为它每次只会根据到源点的距离,选取距离最近的一个节点加入,所以有没有方向都无所谓,算法只关注可达点的距离;至于有环图,它对每个节点的距离计算只用了一层遍历去做,并不会陷入死循环,也不会出现重复计算的问题。因此迪杰斯特拉算法是可以用在无向图和有环图中的,适合于求单源最短路径。
