图的本质是多叉树

图是由节点和边构成的，逻辑结构如下

/* 图节点的逻辑结构 */
class Vertex {
    int id;
    Vertex[] neighbors;
}

对比多叉树：

/* 基本的 N 叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

度（degree） 在无向图中，「度」就是每个节点相连的边的条数。 由于有向图的边有方向，所以有向图中每个节点「度」被细分为入度（indegree）和出度（outdegree）

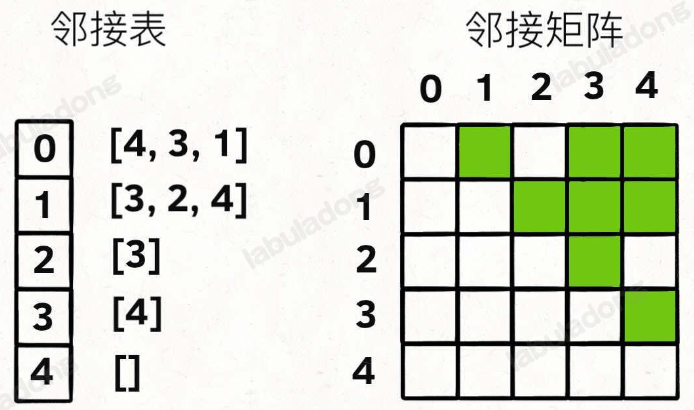
有向无权图

// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
//也可以直接，但不利于输入
int[][] graph;

// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;

有向加权图

// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;

// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重，0 表示不相邻
int[][] matrix;

无向图

无向=双向 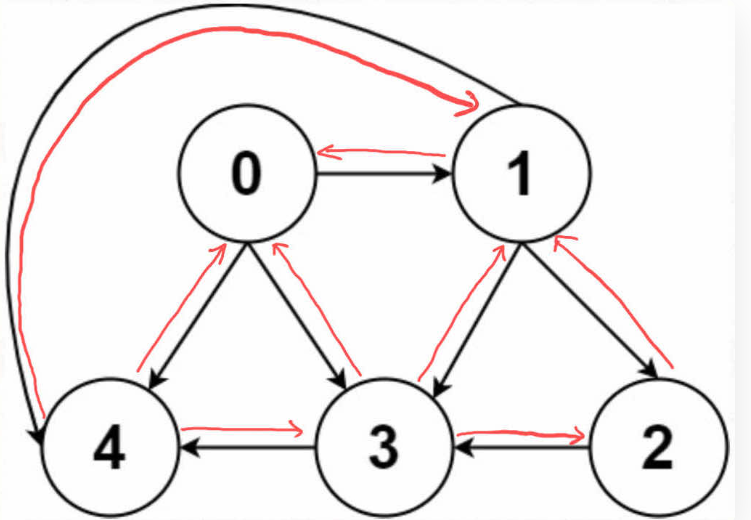如果连接无向图中的节点 x 和 y，把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了；邻接表也是类似的操作，在 x 的邻居列表里添加 y，同时在 y 的邻居列表里添加 x。

图的遍历（参考多叉树）

深度优先算法(DFS)

多叉树的 DFS 遍历框架如下：

/* 多叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;
    // 前序位置
    for (TreeNode child : root.children) {
        traverse(child);
    }
    // 后序位置
}

图和多叉树最大的区别是：图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点，而树不会出现这种情况，从某个节点出发必然走到叶子节点，绝不可能回到它自身。 所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助，防止走回头路

// 记录被遍历过的节点
boolean[] visited;//new boolean[N];
// 记录从起点到当前节点的路径
boolean[] onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {//或遍历每个节点nei->if(matrix[s][nei]==1)
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

可以看出，图的 DFS 就是回溯算法

例如：797. 所有可能的路径 (opens new window)

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序） graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

解法很简单，以 0 为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可。 既然输入的图是无环的，我们就不需要 visited 数组辅助了，直接套用图的遍历框架：

class Solution {
    // 记录所有路径
    List<List<Integer>> res = new LinkedList<>();

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        // 维护递归过程中经过的路径
        LinkedList<Integer> path = new LinkedList<>();
        traverse(graph, 0, path);
        return res;
    }

    /* 图的遍历框架 */
    private void traverse(int[][] graph, int s, LinkedList<Integer> path) {
        // 添加节点 s 到路径
        path.addLast(s);

        int n = graph.length;
        if (s == n - 1){
            // 到达终点
            res.add(new LinkedList<>(path));
            // 可以在这直接 return，但要 removeLast 正确维护 path
            // path.removeLast();
            // return;
            // 不 return 也可以，因为图中不包含环，不会出现无限递归
        }

        // 递归每个相邻节点
        for (int v : graph[s]) {//这里graph存的是相邻节点的序号
            traverse(graph, v, path);
        }

        // 从路径移出节点 s
        path.removeLast();        
    }
}

广度优先算法(BFS)

把一些问题抽象成图，从一个点开始，向四周开始扩散。一般来说，我们写 BFS 算法都是用「队列」这种数据结构，每次将一个节点周围的所有节点加入队列二叉树 (opens new window) BFS 相对 DFS 的最主要的区别是：BFS 找到的路径一定是最短的，但代价就是空间复杂度可能比 DFS 大很多

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构 new LinkedList<>();
    Set<Node> visited; // 避免走回头路 new HashSet<>();或boolean[] visited = new boolean[N];
    
    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (!q.isEmpty()) {
        int size = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < size; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj()) {
                if (!visited.contains(x)) {//或!visited[i]
                    q.offer(x);
                    visited.add(x);
                }
            }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
    return -1;//仍没找到终点返回-1
}

cur.adj() 泛指 cur 相邻的节点；visited 的主要作用是防止走回头路，大部分时候都是必须的，但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要 visited。 例如：111. 二叉树的最小深度 (opens new window) 本题在二叉树的层序遍历中做过

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        // root 本身就是一层，depth 初始化为 1
        int depth = 1;
        
        while (!q.isEmpty()) {
            int sz = q.size();
            /* 将当前队列中的所有节点向四周扩散 */
            for (int i = 0; i < sz; i++) {
                TreeNode cur = q.poll();
                /* 判断是否到达终点 */
                if (cur.left == null && cur.right == null) 
                    return depth;
                /* 将 cur 的相邻节点加入队列 */
                if (cur.left != null)
                    q.offer(cur.left);
                if (cur.right != null) 
                    q.offer(cur.right);
            }
            /* 这里增加步数 */
            depth++;
        }
        return depth;
    }
}

while 循环控制一层一层往下走，for 循环利用 sz 变量控制从左到右遍历每一层二叉树节点